Papers
Published research from my internships and studies at various institutions. My most recent projects were focused on studies of topological phases and criticality using field theory, machine learning, persistent homology and standard numerical (Monte Carlo and tensor network) techniques.
Solvable models for 2+1D quantum critical points
We construct a class of solvable models for 2+1D quantum critical points by attaching 1+1D conformal field theories (CFTs) to fluctuating domain walls forming a loop soup. Specifically, our local Hamiltonian attaches gapless spin chains to the domain walls of a triangular lattice Ising antiferromagnet. The macroscopic degeneracy between antiferromagnetic configurations is split by the Casimir energy of each decorating CFT, which is usually negative and thus favors a short loop phase with a finite gap. However, we found a set of 1D CFT Hamiltonians for which the Casimir energy is effectively positive, making it favorable for domain walls to coalesce into a single snake which is macroscopically long and thus hosts a CFT with a vanishing gap. The snake configurations are geometrical objects also known as fully-packed self-avoiding walks or Hamiltonian walks which are described by an $\mathrm{O}(n=0)$ loop ensemble with a non-unitary 2+0D CFT description. Combining this description with the 1+1D decoration CFT, we obtain a 2+1D theory with unusual critical exponents and entanglement properties. Regarding the latter, we show that the $\log$ contributions from the decoration CFTs conspire with the spatial distribution of loops crossing the entanglement cut to generate a non-local area law. Our predictions are verified by Monte Carlo simulations.
- Co-authors: Amin Moharramipour, Thomas Scaffidi
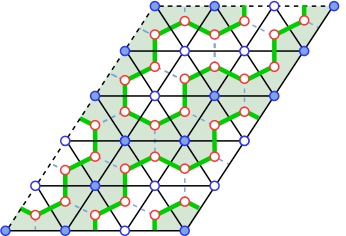
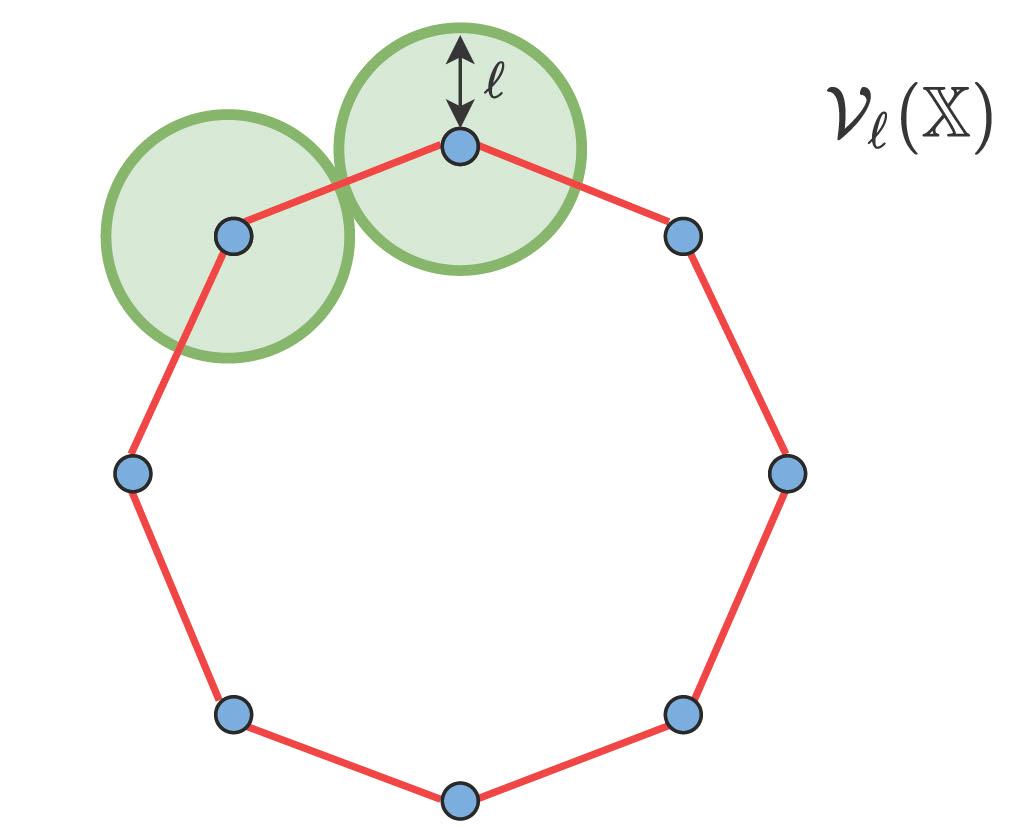
Persistent Homology of $\mathbb{Z}_2$ Gauge Theories
Topologically ordered phases of matter display a number of unique characteristics, including ground states that can be interpreted as patterns of closed strings in the case of general $\mathbb{Z_2}$ string liquids. In this paper, we consider the problem of detecting and distinguishing closed strings in Ising spin configurations sampled from the classical $\mathbb{Z_2}$ gauge theory. We address this using the framework of persistent homology, which computes the size and frequency of general loop structures in spin configurations via the formation of geometric complexes. Implemented numerically on finite-size lattices, we show that the first Betti number of the Vietoris-Rips complexes achieves a high density at low temperatures in the $\mathbb{Z_2}$ gauge theory. In addition, it displays a clear signal at the finite-temperature deconfinement transition of the three-dimensional theory. We argue that persistent homology should be capable of interpreting prominent loop structures that occur in a variety of systems, making it a useful tool in theoretical and experimental searches for topological order.
- Co-authors: Roger G. Melko
- Journal: Physical Review B
- Publication Date: August 8, 2022
Charge Density Waves in Weyl Semimetals
We present a theory of charge density wave (CDW) states in Weyl semimetals and their interplay with the chiral anomaly. In particular, we demonstrate a special nature of the shortest-period CDW state, which is obtained when the separation between the Weyl nodes equals exactly half a primitive reciprocal lattice vector. Its topological properties are shown to be distinct from all other Weyl CDW states. We make a connection between this observation and the three-dimensional fractional quantum Hall state, which was recently proposed to exist in magnetic Weyl semimetals.
- Co-authors: Manisha Thakurathi, Anton A. Burkov
- Journal: Physical Review B
- Publication Date: September 28, 2020
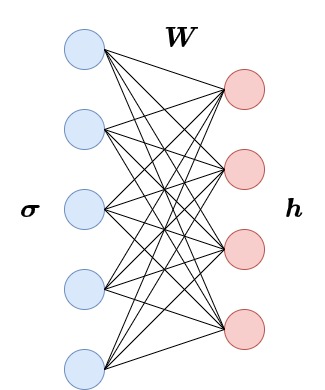
Learnability scaling of quantum states: Restricted Boltzmann machines
Generative modeling with machine learning has provided a new perspective on the data-driven task of reconstructing quantum states from a set of qubit measurements. As increasingly large experimental quantum devices are built in laboratories, the question of how these machine learning techniques scale with the number of qubits is becoming crucial. We empirically study the scaling of restricted Boltzmann machines (RBMs) applied to reconstruct ground-state wave functions of the one-dimensional transverse-field Ising model from projective measurement data. We define a learning criterion via a threshold on the relative error in the energy estimator of the machine. With this criterion, we observe that the number of RBM weight parameters required for accurate representation of the ground state in the worst case – near criticality – scales quadratically with the number of qubits. By pruning small parameters of the trained model, we find that the number of weights can be significantly reduced while still retaining an accurate reconstruction. This provides evidence that overparametrization of the RBM is required to facilitate the learning process.
- Co-authors: A. Golubeva, M. S. Albergo, B. Kulchytskyy, G. Torlai, and R. G. Melko
- Journal: Physical Review B
- Publication Date: November 15, 2019
Multipole Tuning Algorithm for the CANREB HRS at Triumf
The TRIUMF CANadian Rare isotope facility with Electron Beam ion source (CANREB) High Resolution Separator (HRS) has been designed to separate rare isotopes with mass/charge differences of only one part in 20,000 for beams with transverse emittances of 3μm. To reach this resolution, high-order aberrations must be corrected using a multipole corrector. From experience, tuning such a multipole is very challenging. The unique geometry of our multipole motivated a novel tuning method based on determining the desired pole voltages directly from measured emittance. This novel tuning algorithm is presented alongside a web application which has been developed in anticipation of the commissioning of the HRS.
- Co-authors: R. Baartman, C. Barquest, J. Maloney, M. Marchetto, and T. Planche
- Journal: IPAC 2019 Conference Proceedings
- Publication Date: April 29, 2018